Question 83 - Review - Chapter 1

Problem:

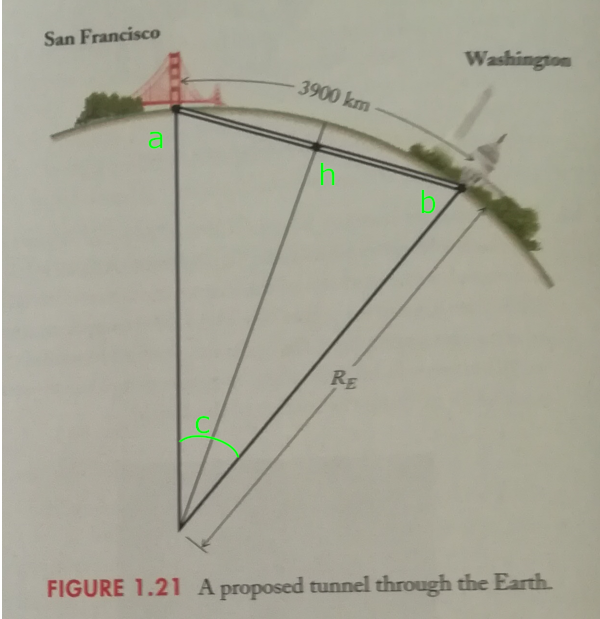
Some engeneers have proposed that for long-distance travel between cities, we should dig perfectly straight connecting tunnels trough the earth (see Fig. below).

A train running along such a tunnel would initialy pick up speed in the first half of the tunnel as if running downhill - it would have maximum speed at the midpoint of the tunnel - and would than gradualy slow down in the second half of the tunnel as if running uphill.

Suppose that such a tunnel were dug between San Francisco and Washington D.C. The distance between those cities measered along the Earth surface is 3900 km.

Question:

a) What is the distance along the straight tunnel?
b) What is the depth at the midpoint of the tunnel, somewhere below Kansas?
c) What is the downward slope of the tunnel on the horisontal direction at San Francisco?

Solution:

First we gonna determine the angle $\widehat{c}$ - The whole circumference of the Earth is $2 * \pi * Radius_{Earth}$

$ \begin{align*} & \widehat{c} = \frac{Radius * 2 * \pi}{Distance * 2 * \pi} = \frac{Radius}{Distance} \end{align*} $

# Calculations
import numpy as np
from astropy.constants import R_earth
Distance = 3900 * 1000 # in m
c = Distance / R_earth.value
print(f'The angle c in rad is {c} rad')

The angle c in rad is 0.6114673648892304 rad

The triangel $\bigtriangleup{ahc}$ is a rectangular triangle with as rectangular $\widehat{cha}$. The side lenght of $|ca| =$ the Radius of the Earth so the length of $|ah| = Radius * \sin{\frac{c}{2}}$ and the length of $|ch| = Radius * \cos{\frac{c}{2}}$

The length of $|ab| = |ah| * 2$

ca = R_earth.value
ah = np.sin(c/2) * ca
ch = np.cos(c/2) * ca
ab = ah * 2
print(f'\ta) The length of |ab| is the length of the tunnel = {ab:.0f} m -or- {ab / 1000:.0f} km')

	a) The length of |ab| is the length of the tunnel = 3839526 m -or- 3840 km

The depth at middelpoint h = $Radius_{Earth} - |ch|$

dept = ca - ch
print(f'\tb) The depth at point h is {dept:0.1f} m -or- {dept / 1000:.0f} km')

	b) The depth at point h is 295775.6 m -or- 296 km

The angle of $|ca|$ with the tangent of a Earth-circle is perpendicula so $\frac{\pi}{2} rad$

The sum of the angles of the triangle $\bigtriangleup{ahc}$ is like all triangles $= \pi rad$

The angle $\widehat{cha} = \frac{\pi}{2}$ so the sum of $\widehat{cah} + \widehat{ach} = \frac{\pi}{2}$

$$\Rightarrow \widehat{cah} = \frac{\pi}{2} - \widehat{ach}$$

The angle of decsent of the tunnel $= \frac{\pi}{2} - \widehat{cah}$

$$\Rightarrow decsent = \frac{\pi}{2} - \frac{\pi}{2} - \widehat{ach}$$

$$\Rightarrow decsent = \widehat{ach}$$

$$\Rightarrow decsent = \frac{\widehat{c}}{2}$$

descent = c / 2
print(f'\tc) The angle of descent is {c/2:0.6f} rad -or- {c*180/(np.pi*2):0.2f}° ')
print(f'\t   The slope is tan(angle) = {np.tan(c/2):.3f}')

	c) The angle of descent is 0.305734 rad -or- 17.52° 
	   The slope is tan(angle) = 0.316